ブログ、日々更新中　カテゴリー：実感算数

こんにちは、教室長の佐田です

先週の土曜日は、小２の男の子と女の子の授業でした。

実感算数も後半を迎え、今まで培ってきた数量感覚や四則計算の本質的な意味、構成把握能力を十分に活用しながら理解を深めてくれています。

 

まずは小数の学習に入った女の子から。

分数の単元を経てきているため、様々な切り口で小数を捉えてくれています。

 

小数のたし算・ひき算では、年長～１年生時にドット棒を使い、１が１０個集まると１０、１０が１０本集まると１００になるという十進法での数量感覚を十分身に着けていますので、

【１．  ２－０．９６】のような計算は、

→１から０．９６を引くと０．０４残る

→残った０．２と０．０４をたすと０．２４

と減加法を使って考えてくれています。

 

わざわざひっ算に書き直したり、数の大きさを見ずに位がずれてしまうことがないのですね。

 

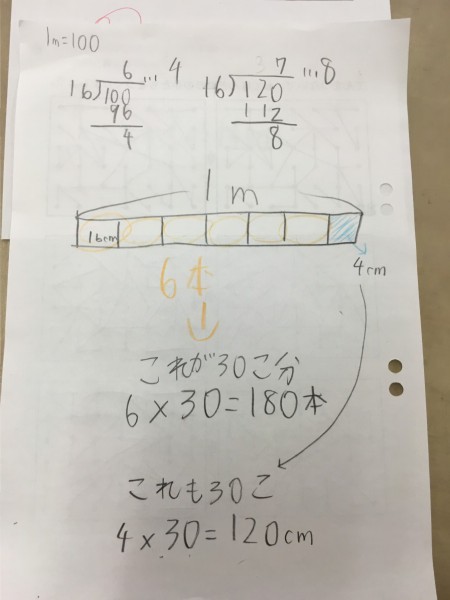
また、下記のような小数の単位変換もこの通り。

 

私、全く説明しておりません！

１ｋｍ＝１０００ｍ、０．１が１０個集まると１になるので、０．１ｋｍ＝１００ｍ

１時間＝６０分、０．１が１０個集まると１になるので、ん～…０．１時間＝６分！

と発見した時にとても嬉しそうな顔を見せてくれました。

また、０．５Lは１Lの半分だから５ｄLだそうです。ここで分数の学習が活かされていますね。

 

次に、小２の男の子は図形の学習。今回は四角形の特徴について。

このプリントに入る前に、十分に作図を通して図形の特徴を体感してもらっています。

 

台形の角を求める際、平行四辺形と違い、対角が等しくないことに気が付きました。

そこで折り紙を使い、同側内角の和が１８０°になること発見！

実際に自分の手を動かして発見したものは、単に暗記したもではなく、経験としてしっかり“記憶”に残りますね。

 

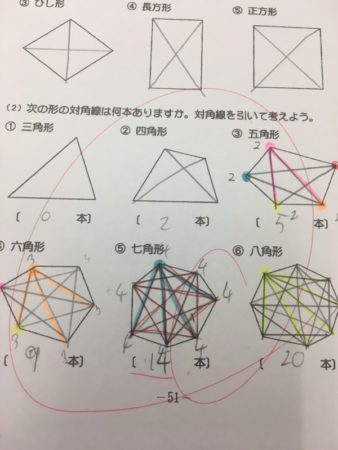
その後の多角形の対角線の本数を求める問題も、試行錯誤を繰り返しながらその法則を見つけてくれました。

 

毎週、新たな発見をしてくれるこの二人。来週も楽しみに待っているよ～!(^^)!

 

 

マネージャーの平井です。

新実感算数カリキュラムになって、新しくプラス学材がカリキュラムに入ってきました。

その中にある「単位量と速さ」

速さといえば、「道のり＝速さ×時間」「時間＝道のり÷速さ」「速さ＝道のり÷時間」の公式を一生懸命覚えた記憶が私にはあります。（しかも意味など全く考えずに、とにかく覚えるという状態でした・・・）

ところが、実感算数で学んでいる子たちは、そんな「公式を必死で覚える」ようなことは全く必要ありません。

カリキュラムに則り、進めていくと「自ら考える姿勢」が育っていますので、ごくごく当たり前のように速さを求め、時間を求め、道のりを導き出します。

先日の小3生との実感算数でも、「平均の速さ」「旅人算」を進めていると、何も苦にすることなくスラスラと解き進めてしまいました。

 

ここれまでの教育はまずは「公式をしっかり覚えましょう」ですが、実感算数の醍醐味はその公式を「自ら獲得するところ」。

そういえば、過去この単元でつまずく子は一人もいませんでしたし、実感算数上がりの小4～6年生に速さ単元で「公式を覚え込ませる」必要はありませんでした。

小学低学年時に自ら考える姿勢、論理的思考力が育てば、後々が全く違ってくることを実感しています。

 

 

こんにちは、今日は、１年生から３年生対象の実感算数の授業の様子についてお話します。

今日は、小学２年生の男の子が、水かさの単元に入りました。

≪水かさ≫は、高学年になっても、一生懸命暗記した内容（１L＝１００ｍL？１０００ｍL？）を思い出そうとしている子が多くみられる苦手意識が強い子が多い単元ですね。

 

でも

実感算数で≪水かさ≫を学習した子は、みんな水かさが大好きなんです。

その理由がこちら↓

 

１０ｍLを喉で味わいます。１０ｍLは一口でなくなってしまうので物足りないですね。

次にこの１０ｍLの計量カップ１０個分で１ｄLになるということを実際に水を移し替えながら見ていきます。

１ｄLを作った後は、また１ｄL分のジュースを飲んでもらいました。

H君は、「ゴクゴクゴクって、ちょうど１０回で飲めたよ！」

と嬉しそうに教えてくれました。もうこれで彼の中で１０ｍLが１０個分＝１００ｍL＝１ｄLの認識が経験から身につきましたね。

これを１Lまで繰り返すと、

「えぇ～！！！次これ飲むの？」と１Lの計量カップに注がれた水を見て驚いていました。

１Lはたくさんすぎて飲めそうもない量だということもしっかり認識できました。

 

たっぷり喉と目で水かさの量認識ができるようになったあとは、様々な問題に触れて理解を深めます。

今日初めて水かさのｍLやｄLの単位を学んだ２年生の子が、１時間の学習が終わるころには、計量カップを片手にこれだけの問題を楽しそうに解いてくれました。

 

 

授業の最後には、「はぁ～楽しかった～」ととても充実し満足そうな笑顔を見せてくれました。

２年生のお子様は、これから秋にかけ、水かさやかけ算の学習にどんどん進んでまいります。

重要な単元が多い学年ですが、実感算数で楽しく新しい発見をしてくれることを楽しみにしています

 

 

全国統一小学生テストとは

小学生が全国のライバルとの競争の中で自分自身と向き合い、 努力をする原点として、
多くのご父母、お子様から賛同を得ている民間による日本最大の小学生テストです。
前回は、全国141,383人の小学生が挑戦しました。

アビリティは、第1回から公認会場として参加しています。

その全国統一小学生テストへは、
普段取り組んでいる小学部のプログラムのアウトプットの場として、

また、テストという場面に向かって少し緊張感も持ちながら目一杯頭を使う年に2回の機会として、

という趣旨にて第1回目からアビリティは公認会場として参加しています。

県内の成績で見れば、
福島県では、
各学年の総合1位は、ほとんどがアビリティ生！

宮城県でも、
算数県内1位、県内一ケタ、全国1位（満点！）
国語県内一ケタ
総合県内一ケタ
といった具合に対応できる子たちが、
回を重ねる毎に続々生まれています。

仙台でも、アビリティの取り組みが成果となって表れてきています。

そして、各学年全国上位５０名が招待されて開催される「全国決勝大会」への進出者が、
アビリティから6回連続で生まれてくれています。

これは、全国のバリバリ中学受験組を相手に、
東北からは異色の存在と勝手に自負しております！

しかしながら、成績と結果がすべての学年ではありません。
あくまで、テストという機会を刺激として一人一人伸びてもらうことが目的です。

そういった意味でのチャレンジを、今回もお待ちしております。

 

 

こんにちは。教室長の佐田です。

今日は、幼児～実感算数と３年目に入る小学２年生の男の子との授業です。

わり算の学習をこの２か月進めてきましたが、今日は最後のまとめの文章題に取り組みました。

 

（２）の問題

「長さ３０ｍのテープを１６ｃｍずつに切り分けます。このとき、テープは何本できて、何ｃｍあまりますか。」

 

この問題は、

“３０÷１６＝１・・・１４”

と言うように単位を見ずに答えてしまう間違いがよく見られますね。

今日の私も、「単位をよく見てみようね」の一言を、心の中に用意していました。

がっ！

Ｈ君は、この問題を読み終わった後、一度３０ｍと式を書こうとしたところで手を止め、

「１ｍだと１００ｃｍだから、６本作れるのか～」

と一言ポツリとつぶやきました。

このメモ、わかりますか？

まず、３０ｍと１６ｃｍの大きさの違いに気が付いたＨ君は、自分で考え易い様に１ｍごとにしてみようと思いついたそうです。

１ｍ＝１００ｃｍだから、１００ｃｍ÷１６ｃｍ＝６本・・・４ｃｍ

これが３０個分なので

６本×３０＝１８０本

ここであまり４ｃｍの存在に気が付きます。

４ｃｍ・・・・・これも３０個ある！と気が付くと

４ｃｍ×３０個＝１２０ｃｍ

１２０ｃｍ÷１６ｃｍ＝７本・・・８ｃｍ

 

よって答えは、１８７本になり、あまりは８ｃｍ

ここまでこの１問に１０分かかりました。

最初の時点で私があの一言を彼に伝えてしまっていたら、３分で終わったかもしれません。

しかしこの１０分間で彼は、数量、わり算の答えの意味、あまりの数が表すものについて、今まで学習してきたことを基に自ら考え導き出してくれました。

彼の自信にも繋がったようです。

少し難しそうな問題に出会ったとき、今までの経験や積み重ねてきた学力を使い、一つ一つ解決していく。この今までの経験を次のステップに自分から発展させることができるようになってくると、また一段と学習への意欲が高まりますね。

次の単元の学習でも、どんな成長を見せてくれるのか、楽しみです。