この仙台の地でも、いよいよ小4までに中2レベルの算数・数学力を養うスーパーピグマリオン講座が開講致します
マナビのマキバ教室では、この4月より、東北地方で初の
小4までに中2レベルの算数・数学力を養う
「スーパーピグマリオン講座」
を開講致します。
このスーパーピグマリオンは、幼児年少期から小学4年生までかけ、今までピグマリオンが創りあげてきたノウハウ全てを使いお子様の能力を引き出し、高い知性と能力を育てます。
仙台教室では、年少児からスタートし、
指先能力、空間能力、合成分解能力、全体把握能力、注意力、構成把握能力、図形形態認識能力などをバランスよく育てながら、
年少(20までの数の認識)/年中(100までの数の認識)/年長(1000までの数の認識)
最終的に小学4年生で中2数学終了までの内容を指導します。
また、指導学材の枚数も、従来のピグマリオン講座の月64ページ前後から、3倍の180ページ以上になります。
単なる詰め込み式の教える教育ではなく、自ら学ぶ学育により、無理なく、それぞれの能力を見極めながら本物の学力を育てる講座です。
こちらは、年少クラス(残り1席)、年中クラス(残り2席)の限定となりますのでお早めにお問い合わせください。
また、
幼児期に能力の発達段階に合わせて、お子さまが自ら感じ、考え、学ぶ力を育てる
「幼児ピグマリオン講座」年少~年中クラス(残席わずか)
小学校入学前に20までの数認識と考える力の基礎を築く
「幼児ピグマリオン講座」年長クラス
県内トップ層・東北1位・全国上位50人による決勝大会進出者を輩出し続けている
小学1~3年生対象「新・実感算数」
も、4月生を募集しております。
定員になってしまったお時間もございますので、お早目にこちらもお問い合わせください。








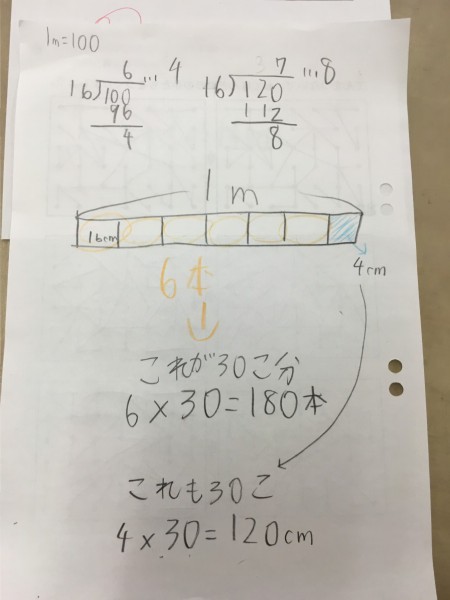

 (分母をかけて分子で割る=逆数をかける ですよね
(分母をかけて分子で割る=逆数をかける ですよね