分数の割り算は、なぜ逆数にしてかけるのでしょう?図を描いて手と頭を使って考える実感算数だと理解も早い!
こんにちは![]()
スタッフの永浦です![]()
分数の割り算は、なぜ逆数にしてかけるのでしょう?
お子さんに聞かれて困ったことはありませんか?
実感算数では、紙テープを切ったり、図に描いたりしながら意味を理解していきます。
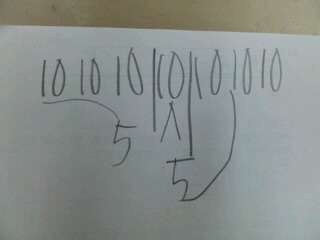
2÷3/7=14/3=4と2/3を例にとって考えてみましょう。
まず、意味を考えると、「2を『7分の3』ずつに分けること」ですよね。
2本の紙テープをそれぞれ7等分して『7分の1』を作ります。
すると、『7分の1』が1本につき7個、合計、2×7個できますね(分母の数をかけています。)

『7分の3』ずつに分けるから、『7分の1』を3個ずつに分けていきます。(分子の数で割っています。)
 (分母をかけて分子で割る=逆数をかける ですよね
(分母をかけて分子で割る=逆数をかける ですよね![]() )
)
すると、『7分の3』が4個と余り(『7分の2』)ができます。
余りの『7分の2』は『7分の3』の3分の2にあたります。
こんな説明をしてから、小学3年生の女の子に自分でも図に描きながら解いてもらいました。

実際に自分で描くことにより、なんとなくの理解からしっかりした理解に変わっていきます。
一問、一問ていねいに、なぜ逆数をかければ良いのか図を使って説明してくれました![]()